|
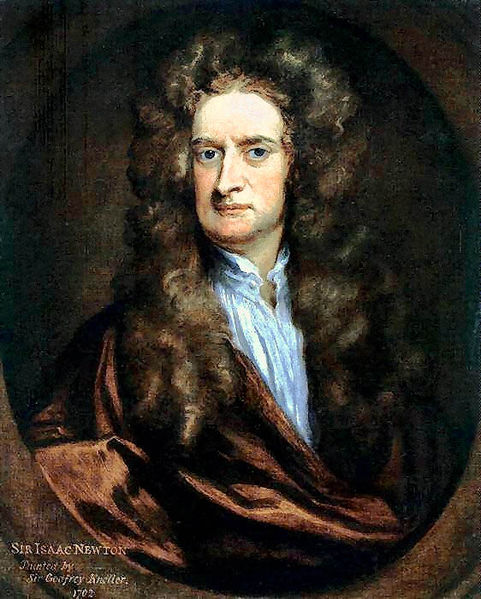
Isaac Newton
Sir Isaac Newton, (4 de
enero, 1643 NS – 31 de marzo, 1727 NS) fue un científico, físico, filósofo, alquimista y matemático
inglés, autor de los Philosophiae Naturalis Principia Mathematica,
más conocidos como los Principia, donde describió la ley de gravitación universal
y estableció las bases de la Mecánica Clásica mediante las leyes
que llevan su nombre. Entre sus otros descubrimientos científicos destacan los trabajos sobre la naturaleza de la luz y la óptica (que se presentan principalmente en el Opticks) y el desarrollo del cálculo matemático.
Newton fue el primero en demostrar que las leyes naturales
que gobiernan el movimiento en la Tierra y las que gobiernan el movimiento de los cuerpos
celestes son las mismas. Es, a menudo, calificado como el científico más grande de todos
los tiempos, y su obra como la culminación de la Revolución científica.
Entre sus hallazgos científicos se encuentran los siguientes:
el descubrimiento de que el espectro de color que se observa cuando la luz blanca pasa por un prisma es inherente a esa luz, en lugar de provenir
del prisma (como había sido postulado por Roger Bacon en el siglo
XIII); su argumentación sobre la posibilidad de que la luz estuviera compuesta por partículas;
su desarrollo de una ley de conducción térmica, que describe la tasa de enfriamiento de
los objetos expuestos al aire; sus estudios sobre la velocidad
del sonido en el aire; y su propuesta de una teoría sobre el origen de las estrellas.
Newton comparte con Leibniz
el crédito por el desarrollo del cálculo integral y diferencial, que utilizó para formular
sus leyes de la física. También contribuyó en otras áreas de las matemáticas,
desarrollando el teorema del binomio. El matemático y físico matemático Joseph Louis Lagrange (1736–1813), dijo que "Newton fue el más grande genio que ha existido y también
el más afortunado dado que sólo se puede encontrar una vez un sistema que rija al mundo."
Biografía
Nació el 25 de diciembre de 1642 (correspondiente al 4 de enero de 1643 del nuevo calendario) en Woolsthorpe, Lincolnshire, Inglaterra; fue hijo de dos campesinos
puritanos, aunque nunca llegó a conocer a su padre, pues había muerto en octubre de 1642. Cuando su madre volvió a casarse,
lo dejó a cargo de su abuela, con quien vivió hasta la muerte de su padrastro en 1653. Realizó estudios en la Free Grammar School en Grantham y a los dieciocho
años ingresó en la Universidad de Cambridge para continuar sus
estudios. Su primer tutor oficial fue Benjamín Pulleyn. Newton nunca asistió regularmente
a sus clases, ya que su principal interés era la biblioteca. Se graduó en el Trinity College
como un estudiante mediocre debido a su formación principalmente autodidacta, leyendo algunos de los libros más importantes
de matemáticas y filosofía natural de la época. En 1663 Newton leyó la Clavis
mathematicae de William Oughtred, la
Geometría de Descartes, de Frans van
Schooten, la Óptica de Kepler, la
Opera mathematica de Viète, editadas por Van Schooten y, en 1664, la
Aritmética de John Wallis, que le serviría como introducción a sus
investigaciones sobre las series infinitas, el teorema del binomio
y ciertas cuadraturas.
En 1663
conoció a Isaac Barrow, quien le dio clase como
su primer profesor Lucasiano de matemáticas. En
la misma época entró en contacto con los trabajos de Galileo, Fermat, Huygens y otros a partir, probablemente, de la edición de 1659 de la Geometría
de Descartes por Van Schooten. Newton superó rápidamente
a Barrow, quien solicitaba su ayuda frecuentemente en problemas matemáticos.
En
esta época la geometría y la óptica ya tenían un
papel esencial en la vida de Newton. Fue en este momento en que su fama comenzó a crecer ya que inició una correspondencia
con la Royal Society (Sociedad Real). Newton les envió algunos de sus descubrimientos
y un telescopio que suscitó un gran interés de los
miembros de la Sociedad, aunque también las críticas de
algunos de sus miembros, principalmente Robert Hooke.
Esto fue el comienzo de una de la muchas disputas que tuvo en su carrera científica. Se considera que Newton demostró agresividad
ante sus contrincantes que fueron principalmente, (pero no únicamente) Hooke, Leibniz y, en lo religioso, la Iglesia de Roma. Cuando fue presidente de
la Royal Society, fue descrito como un dictador cruel, vengativo y busca-pleitos. Sin embargo,
fue una carta de Robert Hooke, en la que éste comentaba sus ideas intuitivas acerca de la gravedad, la que hizo que iniciara
de lleno sus estudios sobre la mecánica y la gravedad.
Newton resolvió el problema con el que Hooke no había podido y sus resultados los escribió en lo que muchos científicos creen
que es el libro más importante de la historia de la ciencia, el Philosophiae
Naturalis Principia Mathematica.
En 1693
sufrió una gran crisis psicológica, causante de largos periodos en los que permaneció aislado, durante los que no comía ni
dormía. En esta época sufrió depresión y arranques
de paranoia. Mantuvo correspondencia con su amigo,
el filósofo John Locke, en la que, además de contarle
su mal estado, lo acusó en varias ocasiones de cosas que nunca hizo. Algunos historiadores creen que la crisis fue causada
por la ruptura de su relación con su discípulo Nicolás Fatio de Duillier; la mayoría, sin embargo, opina que en esta época Newton se había envenenado al hacer sus experimentos alquímicos. Después de escribir los Principia abandonó
Cambridge mudándose a Londres donde ocupó diferentes puestos públicos de prestigio siendo nombrado
Preboste del Rey, magistrado de Charterhouse y director de la Casa de Moneda.
Entre sus intereses más profundos se encontraban la alquimia y la religión, temas en los que sus escritos sobrepasan con mucho en volumen sus escritos científicos. Entre sus opiniones religiosas
defendía el arrianismo y estaba convencido de que
las Sagradas Escrituras habían sido violadas para
sustentar la doctrina trinitaria. Esto le causó
graves problemas al formar parte del Trinity College en Cambridge y sus ideas religiosas impidieron que pudiera ser director
del College. Entre sus estudios alquímicos estaba interesado en temas esotéricos como la transmutación de los elementos, la
piedra filosofal y el elixir de la vida.
Primeras contribuciones
Desde finales de 1664 trabajó intensamente en diferentes problemas
matemáticos. Abordó entonces el teorema del binomio, a partir de los trabajos de John Wallis, y desarrolló un método propio denominado cálculo de fluxiones. Poco después regresó a la granja familiar a causa de
una epidemia de peste bubónica.
Retirado con su familia durante los años 1665-1666, conoció un período muy intenso de descubrimientos, entre los que destaca la ley del inverso del cuadrado de la gravitación, su desarrollo de las bases de la mecánica clásica, la formalización del método de fluxiones y la generalización
del teorema del binomio, poniendo además de manifiesto la naturaleza física de los colores. Sin embargo, guardaría silencio
durante mucho tiempo sobre sus descubrimientos ante el temor a las críticas y el robo de sus ideas. En 1667 reanudó sus estudios
en Cambridge.
Desarrollo del Cálculo
De 1667 a 1669 emprendió investigaciones sobre óptica y fue elegido fellow
del Trinity College. En 1669 su mentor, Isaac Barrow, renunció a su Cátedra Lucasiana de matemáticas, puesto en el que Newton le sucedería hasta 1696. El mismo
año envió a John Collins, por medio de Barrow, su
"Analysis per aequationes numero terminorum infinitos". Para Newton, este manuscrito representa la introducción a un
potente método general, que desarrollaría más tarde: su cálculo diferencial e integral.
Newton había descubierto los principios de su cálculo diferencial e
integral hacia 1665-1666 y, durante el decenio siguiente, elaboró al menos tres enfoques diferentes de su nuevo
análisis.
Newton y Leibniz protagonizaron una agria polémica sobre la autoría
del desarrollo de esta rama de las matemáticas. Los historiadores de la ciencia consideran que ambos desarrollaron el cálculo
independientemente, si bien la notación de Leibniz era mejor y la formulación de Newton se aplicaba mejor a problemas prácticos.
La polémica dividió aún más a los matemáticos británicos y continentales, sin embargo esta separación no fue tan profunda
como para que Newton y Leibniz dejaran de intercambiar resultados.
Newton abordó el desarrollo del cálculo a partir de la geometría analítica desarrollando un enfoque geométrico y analítico
de las derivadas matemáticas aplicadas sobre curvas definidas a través de ecuaciones. Newton también buscaba cómo cuadrar distintas curvas, y la relación entre la cuadratura y la teoría de tangentes. Después de los estudios de Roberval, Newton se percató de que el método de tangentes podía utilizarse
para obtener las velocidades instantáneas de una trayectoria conocida. En sus primeras investigaciones Newton lidia únicamente
con problemas geométricos, como encontrar tangentes, curvaturas y áreas utilizando como base matemática la Geometría Analítica de Descartes. No obstante, con el afán de
separar su teoría de la de Descartes, comenzó a trabajar únicamente con las ecuaciones y sus variables sin necesidad de recurrir
al sistema cartesiano.
Después de 1666 Newton abandonó sus trabajos matemáticos sintiéndose
interesado cada vez más por el estudio de la naturaleza y la creación de sus Principia.
Trabajos sobre la luz
Entre 1670 y 1672 trabajó intensamente en problemas
relacionados con la óptica y la naturaleza de la luz.
Newton demostró que la luz blanca estaba formada por una banda de colores (rojo, naranja, amarillo, verde, azul y violeta)
que podían separarse por medio de un prisma. Como
consecuencia de estos trabajos concluyó que cualquier telescopio refractor sufriría de un tipo de aberración conocida en la actualidad como aberración
cromática que consiste en la dispersión de la luz en diferentes colores al atravesar una lente. Para evitar este problema inventó un telescopio reflector (conocido como telescopio newtoniano).
Sus experimentos sobre la naturaleza de la luz le llevaron a formular
su teoría general sobre la misma que, según él, está formada por corpúsculos y se propaga en línea recta y no por medio de ondas. El libro en que expuso esta teoría fue severamente criticado por la mayor parte de sus contemporáneos, entre ellos
Hooke (1638-1703) y Huygens, quienes sostenían ideas diferentes defendiendo una naturaleza ondulatoria. Estas
críticas provocaron su recelo por las publicaciones, por lo que se retiró a la soledad de su estudio en Cambridge.
En 1704 Newton escribió su obra más importante sobre óptica, Opticks, en la que exponía sus teorías anteriores y la naturaleza corpuscular de la luz, así como un estudio detallado sobre
fenómenos como la refracción, la reflexión y la dispersión de la luz.
Aunque sus ideas acerca de la naturaleza corpuscular de la luz pronto
fueron desacreditadas en favor de la teoría ondulatoria, los científicos actuales han llegado a la conclusión (gracias a los
trabajos de Max Planck y Albert Einstein) de que la luz tiene una naturaleza dual: es onda y corpúsculo
al mismo tiempo. Esta es la base en la cual se apoya toda la Mecánica Cuántica.
Ley de gravitación universal
Bernard Cohen afirma que “El
momento culminante de la Revolución científica fue el descubrimiento
realizado por Isaac Newton de la ley de la gravitación universal.” Con una simple ley, Newton dio a entender los fenómenos físicos más importantes del universo
observable, explicando las tres leyes de Kepler. Le ley de la gravitación universal descubierta
por Newton se escribe

donde F es la fuerza, G es una constante que determina
la intensidad de la fuerza y que sería medida años más tarde por Henry Cavendish en su célebre experimento de la balanza de torsión, m1 y m2 son las masas de dos cuerpos que se atraen entre sí y r es la
distancia entre ambos cuerpos, siendo el
vector unitario que indica la dirección del movimiento.
La ley de gravitación universal nació en 1685 como culminación de una serie de estudios y trabajos iniciados mucho antes.
En 1679 Robert Hooke introdujo a Newton en el problema
de analizar una trayectoria curva. Cuando Hooke se convirtió en secretario de la Royal Society quiso entablar una correspondencia filosófica con Newton. En su primera
carta planteó dos cuestiones que interesarían profundamente a Newton. Hasta entonces científicos y filósofos como Descartes
y Huygens analizaban el movimiento curvilíneo con
la fuerza centrífuga, sin embargo Hooke proponía
“componer los movimientos celestes de los planetas a partir de un movimiento rectilíneo a lo largo de la tangente y un movimiento atractivo, hacia el cuerpo central.”
Sugiere que la fuerza centrípeta hacia el Sol varía
en razón inversa al cuadrado de las distancias. Newton contesta que él nunca había oído hablar de estas hipótesis.
En otra carta de Hooke, escribe: “Nos queda ahora por conocer
las propiedades de una línea curva... tomándole a todas las distancias en proporción cuadrática inversa.” En otras palabras,
Hooke deseaba saber cuál es la curva resultante de un objeto al que se le imprime una fuerza inversa al cuadrado de la distancia.
Hooke termina esa carta diciendo: “No dudo que usted, con su excelente método, encontrará fácilmente cuál ha de ser
esta curva.”
En 1684 Newton informó a su amigo Edmund Halley de que había resuelto el problema de la fuerza inversamente proporcional al
cuadrado de la distancia. Newton redactó estos cálculos en el tratado “De
Motu” y los desarrolló ampliamente en el libro “Philosophiae Naturalis Principia Mathematica”. Aunque muchos astrónomos no utilizaban
las leyes de Kepler, Newton intuyó su gran importancia
y las engrandeció demostrándolas a partir de su ley de la gravitación universal.
Sin embargo, la gravitación universal es mucho más que una fuerza dirigida
hacia el Sol. Es también un efecto de los planetas
sobre el Sol y sobre todos los objetos del Universo.
Newton intuyó fácilmente a partir de su tercera ley de la dinámica que si un objeto atrae a un segundo objeto, este segundo también atrae al primero con la misma fuerza. Newton se percató
de que el movimiento de los cuerpos celestes no podía ser regular. Afirmó: “los planetas ni se mueven exactamente
en elipses, ni giran dos veces según la misma órbita”. Para Newton, ferviente religioso, la estabilidad de las órbitas
de los planetas implicaba reajustes continuos sobre sus trayectorias impuestas por el poder divino.
Las leyes de la Dinámica
Otro de los temas tratados en sus Principa fueron las tres leyes de la Dinámica o Leyes de Newton, en las que explicaba el movimiento de los cuerpos y sus efectos y causas. Éstas son:
La primera ley de Newton o ley de la inercia
"Todo cuerpo preservará en sus estado de reposo o movimiento uniforme y rectilíneo
a nos ser que sea obligado por fuerzas impresas a cambiar su estado"
En esta ley, Newton afirma que un cuerpo sobre el que no actúan fuerzas extrañas
(o las que actúan se anulan entre sí) permanecerá en reposo o moviéndose con velocidad constante.
Esta idea, que ya había sido enunciada por Descartes y Galileo, suponía romper
con la física aristotélica, según la cual un cuerpo solo se mantenía en movimiento mientras actúe una fuerza sobre él.
La segunda ley de Newton o ley de la interacción y la fuerza
"El cambio de movimiento es proporcional a la fuerza motriz impresa y ocurre según
la línea recta a lo largo de la cual aquella fuerza se imprime"
Esta ley explica las condiciones necesarias para modificar el estado de movimiento
o reposo de un cuerpo. Según Newton estas modificaciones solo tendrán lugar si se produce una interacción entre dos cuerpos,
entrando o no en contacto (por ejemplo, la gravedad actúa sin que haya contacto físico). Según la segunda ley, las interacciones
producen variaciones en el momento lineal, a razón
de
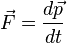
Siendo 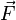 la fuerza, la fuerza, 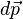 la derivada del momento lineal, dt la derivada del tiempo. la derivada del momento lineal, dt la derivada del tiempo.
La segunda ley puede resumirse en la fórmula,

siendo 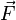 la fuerza (medida en newtons) que hay que aplicar sobre un cuerpo de masa m para provocar una aceleración la fuerza (medida en newtons) que hay que aplicar sobre un cuerpo de masa m para provocar una aceleración  . .
La tercera ley de Newton o ley de de acción-reacción
"Con toda acción ocurre siempre una reacción igual y contraria; las acciones mutuas de dos cuerpos siempre
son iguales y dirigidas en sentidos opuestos"
Esta ley se refleja constantemente en la naturaleza: la sensación de dolor que se siente al golpear una mesa,
puesto que la mesa ejerce una fuerza sobre ti con la misma intensidad; el impulso que consigue un nadador al ejercer una fuerza
sobre el borde de la piscina, siendo la fuerza que le impulsa la reacción a la fuerza que él ha ejercido previamente.
|

